Принятие коллективных решений сопряжено с необходимостью создания коалиций игроков. Если требуется дать количественную оценку влияния каждого, возможно использовать теорию принятия решений и так называемые индексы влияния. Они способны помочь выявить самого влиятельного акционера в совете директоров, партию в парламенте с помощью математических расчетов, снизить долю риска при выборе партнеров, выяснить эффективность принимаемых решений. Как математически определить сильнейшего при помощи индексов влияния, рассказал доцент НИУ ВШЭ Алексей Мячин на лекции осенней школы «Теория принятия решений и другие вопросы современной прикладной математики в экономике».
Как работают индексы влияния
Индексы влияния — это математические инструменты, используемые для оценки влияния участников в различных системах, таких как экономические рынки, политические органы и бизнес-структуры. Индексы имеют корни в теории игр и кооперативной теории, но их применение также распространено в экономике и политике. Работа с индексами началась в 50-х годах XX века, и за прошедшие полвека были разработаны индексы Банцафа, Шепли — Шубика, Джонстона, Дигена — Пакела, Холера — Пакела, Коулмана и другие. Известны также индекс Алескерова и индекс эффективности влияния, предложенные заслуженным профессором НИУ ВШЭ математиком Фуадом Алескеровым.
Чтобы умело оперировать индексами, нужно разобраться в некоторых связанных с ними понятиях, таких как влияние, квота, выигрывающая коалиция и ключевой игрок.
Влияние — это способность оказывать воздействие на ход событий или принятие решений. Наибольшее влияние в парламенте может иметь игрок с большим количеством мест или голосов, за исключением некоторых случаев. Расчет индексов направлен на определение влияния конкретных игроков или же коалиций, в которых они состоят.
Квота — это минимальное необходимое количество голосов для принятия того или иного решения. Механизм квоты реализуется в парламентах и советах директоров: для утверждения законов во многих парламентах мира необходимо набрать простое большинство голосов, т.е. 50% голосов парламентариев и еще один дополнительный голос, создающий перевес в сторону большинства. Другим частным примером квоты является относительное большинство (больше, чем набрали другие игроки), а также конституционное большинство (как правило, две трети плюс один голос).
Выигрывающая коалиция — коалиция, общее число голосов которой равно квоте или превышает ее. То есть такая коалиция в составе определенной комбинации игроков может самостоятельно принять решение без чужой помощи или же заблокировать его в процессе голосования.
Ключевой игрок — участник выигрывающей коалиции, при исключении которого она перестает быть выигрывающей. Без ключевого игрока у коалиции будет недостаточно голосов для принятия решения. Ключевых игроков в одной коалиции может быть несколько. В случае если каждый участник коалиции — ключевой, такая коалиция называется минимально выигрывающей.
Индекс Банцафа
Одним из наиболее часто используемых и несложных для расчета индексов является индекс Банцафа, который был предложен еще в 1965 году. Считается, что его создатель, Джон Банцаф, заинтересовался избирательной системой округа Нассо (штат Нью-Йорк), в котором, по его наблюдениям, разные избиратели не имели равных прав на выборах представителей в местные органы власти. Банцаф разработал специальный индекс и математически доказал свою теорию. Впоследствии проблему с неравным представительством в округе решили, а индекс начал применяться не только в теории игр, но и в реальных политике и экономике.
Результаты расчета индекса Банцафа позволяют оценить возможность определенного участника изменить исход голосования с помощью его влияния в составе коалиций. Этот индекс в качестве основного индекса для примера и использовал Алексей Мячин в ходе лекции.
Формула расчета индекса Банцафа выглядит так:

В расчете индекса Банцафа есть несколько этапов:
- расчет квоты;
- нахождение всех комбинаций выигрывающих коалиций;
- определение, в каких коалициях участник — ключевой;
- расчет доли влияния каждого участника.
Разберемся на примере.
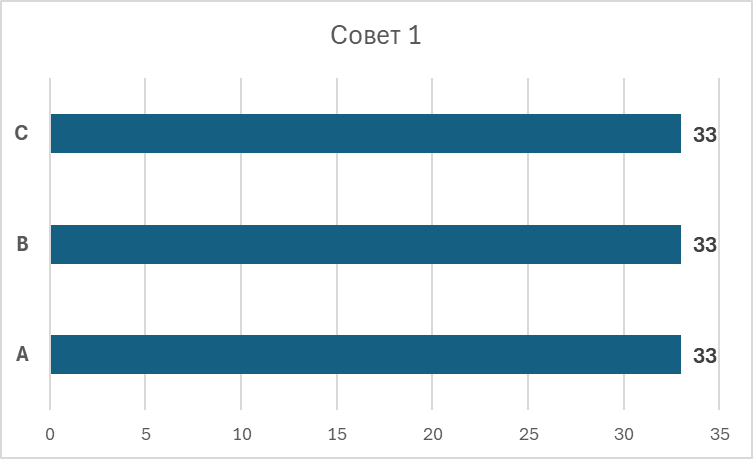
Рис. 1 из презентации А.Л. Мячина
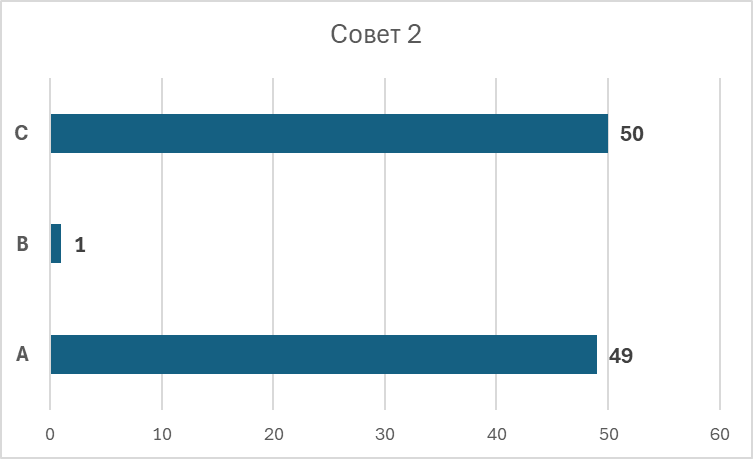
Рис. 2 из презентации А.Л. Мячина
Рассмотрим одновременно два примера с разным распределением голосов. Предположим, что в каждом совете директоров есть три акционера — А, В и С. Общее количество голосов равно 99. В первом совете у каждого из акционеров есть по 33 голоса, во втором совете у игроков А и В — по 48 голосов, а у игрока С — 3 голоса.
Квота равна 50% голосов + 1 дополнительный голос. В обоих рассматриваемых случаях квота для принятия решения будет равна 50 голосам. Поскольку количество голосов каждого акционера по отдельности является недостаточным для преодоления квоты, держателям акций придется договариваться при голосовании и образовывать коалиции.
Выигрывающей коалицией будет считаться та, сумма голосов участников которой равна квоте или превышает ее, т.е. которая набирает 50 голосов или больше. Для точного расчета необходимо найти все комбинации таких коалиций с участием трех акционеров. И в первом, и во втором советах ими будут: А+В (66; 96), А+С (66; 51), В+С (66; 51), А+В+С (99; 99). Мы видим, что, несмотря на совсем разное распределение голосов, коалиции в обоих советах совпадают. Значит, ответ для двух советов будет одинаковый.
Теперь попытаемся вычислить влияние игрока А для обоих случаев. В числителе дроби по формуле нужно будет записать количество коалиций, в которых А — ключевой игрок. Это коалиции А+В и А+С, т.е. два случая. В знаменателе — общее количество случаев в коалициях, в которых есть ключевой игрок. В коалиции А+В ключевые игроки — А и В (2 игрока), в А+С — А и С (2 игрока), в В+С — В и С (2 игрока), в А+В+С никто из игроков не является ключевым. Соответственно, в знаменатель идет 2+2+2 случаев.
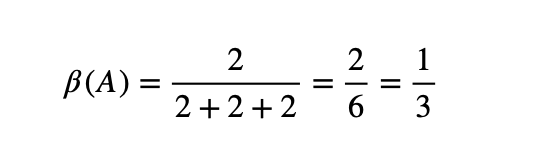
Вычислив влияние игроков В и С по такому же принципу, мы поймем, что влияние игроков А, В и С равнозначно.

Интересно, что во втором совете даже игрок С, владеющий всего 3 голосами, имеет такое же влияние, как и другие акционеры со значительно большим их количеством. Получается, что влияние не всегда напрямую зависит от того, сколько голосов есть у акционера, важно также и их распределение среди других игроков.
Парадоксы индекса Банцафа
При вычислении индекса Банцафа могут, однако, возникнуть некоторые парадоксы. Самыми известными являются парадокс новых игроков и парадокс перераспределения, которым Алексей Мячин уделил особое внимание.
Парадокс новых игроков предполагает, что в случае вхождения в число участников нового игрока влияние старых игроков, по идее, должно уменьшиться. Однако все может произойти и наоборот: за счет перераспределения того же количества голосов/акций между участниками старые игроки могут отдать некое количество своих акций новому игроку и повысить за счет этого собственное влияние. С увеличением круга участников увеличивается и количество выигрывающих коалиций, а следовательно, может возрасти и влияние отдельных игроков.
Парадокс перераспределения возникает, когда какой-то игрок передает часть своих голосов/акций другому и при этом его влияние остается таким же или даже возрастает.
Рассмотрим парадокс перераспределения на следующем примере.
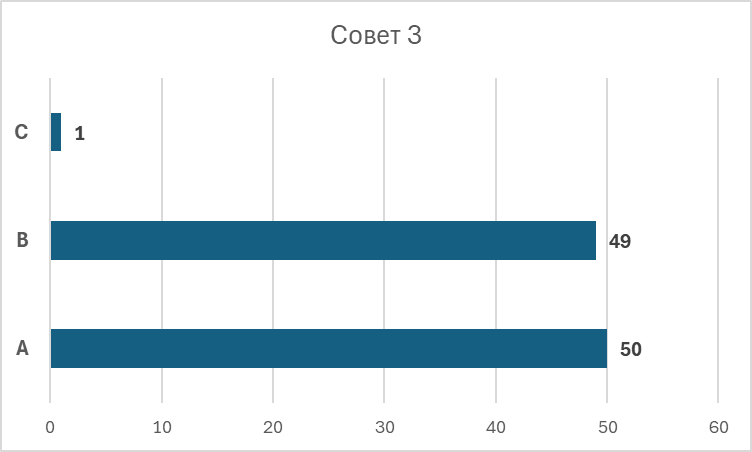
Рис. 3 из презентации А.Л. Мячина
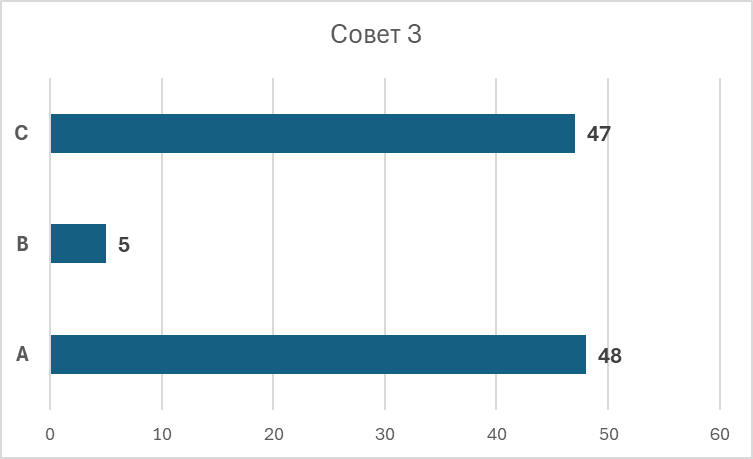
Рис. 4 из презентации А.Л. Мячина
На первом рисунке изображен совет до перераспределения голосов, а на втором рисунке — после, когда игроки А и В отдали игроку С часть своих голосов. Квота в совете равна 51 голосу, так как всего голосов 100.
В первом случае влияние игроков следующее:
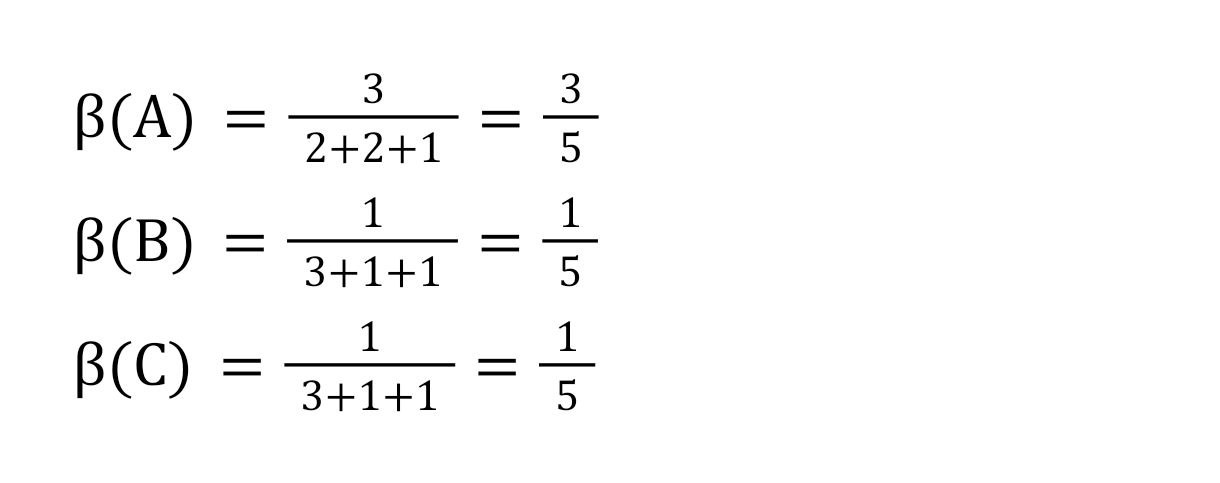
У игрока А — наибольшее влияние.
Рассмотрим второй случай.
Игрок В отдал игроку С 44 своих голоса и сохранил всего 5, тогда как игрок А отдал игроку С всего 2 голоса. Как изменится влияние при таком перераспределении голосов? Может показаться, что влияние игрока В сильно упадет, ведь он лишился большинства своих голосов, но это не так.
В этом случае выигрывающими коалициями являются А+В, А+С, В+С и А+В+С. Из-за понижения своей доли голосов игрок В смог войти в большее количество выигрывающих коалиций, из-за чего его влияние возросло и достигло уровня игроков А и С:
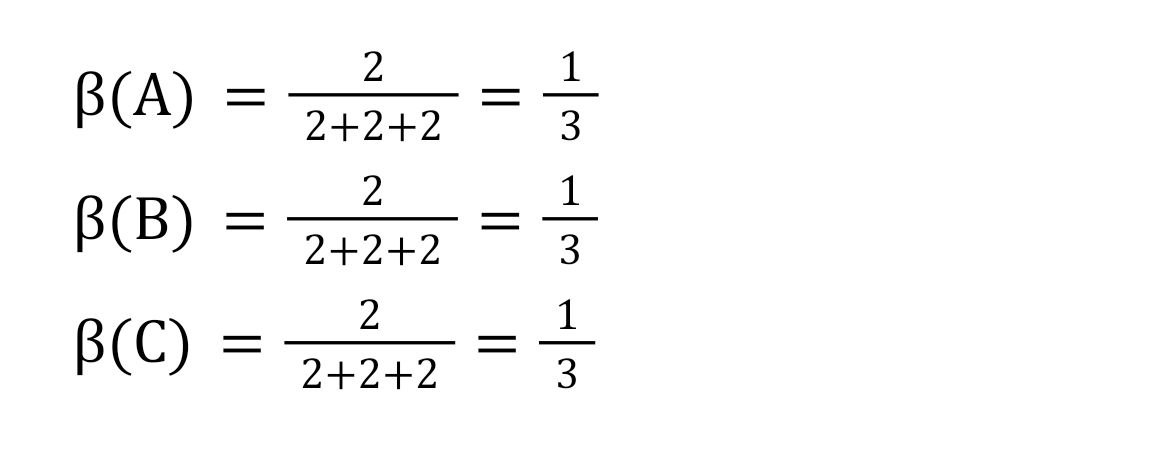
Таким образом, уровень влияния напрямую зависит не от того, мало или много голосов у игрока, а от того, как их количество соотносится с квотой и голосами других участников. Даже мелкие акционеры могут сильно изменить ход голосования, что хорошо видно на примерах.
Индексы влияния могут применяться в бизнес-анализе, политике и других сферах. Математическая оценка рисков бывает особенно полезна там, где всегда нужно следить за настроениями многочисленных акционеров и партнеров, просчитывать их будущие шаги. Индексы влияния могут сделать коллективные процессы более управляемыми, что выгодно бизнесу, который любит предсказуемость, отметил спикер.



